O que é Valor Esperado Positivo (EV) em Apostas Esportivas?

Aposta com Valor Esperado (EV) é uma estratégia de apostas esportivas baseada na busca por uma discrepância entre as verdadeiras probabilidades de algo acontecer e as probabilidades publicadas pela casa de apostas. Valor Esperado (Value Bets) representa a média de dinheiro que um apostador pode esperar ganhar ou perder em uma aposta específica ao longo do tempo. Leva em consideração a probabilidade de ganhar ou perder e o pagamento potencial. Ao calcular o valor esperado, um apostador pode determinar se uma aposta específica é potencialmente lucrativa ou não.

Um valor negativo -EV em apostas esportivas é uma situação em que o retorno esperado da aposta é negativo. Isso significa que a probabilidade de ganhar no jogo é menor do que o esperado.

Um valor positivo +EV em apostas esportivas é uma aposta que será lucrativa a longo prazo. Isso significa que tal aposta ganhará mais do que perderá no longo prazo (por exemplo, apostando consistentemente em probabilidades de -110, você acabará obtendo lucro após 100 apostas). A probabilidade de ganhar essa aposta geralmente é maior do que a assumida pela casa de apostas.

Usando essa estratégia, o jogador perderá algumas apostas. No entanto, a longo prazo, ele ainda sairá à frente. Por isso, é crucial seguir a estratégia até o final.

Uma Explicação Mais Simples com um Exemplo.

Breve explicação das odds americanas:

1. No sistema de odds americanas, o número na linha aumenta à medida que a probabilidade de vitória diminui, e o número na linha diminui à medida que a probabilidade de vitória aumenta.
2. Isso significa que um azarão com +100 tem uma probabilidade maior de vitória do que um azarão com +240 (segundo a casa de apostas). Por outro lado, um favorito com -190 tem uma maior chance de vitória do que um favorito com -120.

Exemplo de uma Aposta com Valor Esperado Negativo (-EV)

Vamos considerar o evento de “jogar uma moeda”. Você jogou uma moeda 100 vezes e, a cada vez, fez uma aposta de $100 em coroa com odds de -110 (uma aposta de $100 resulta em um ganho de $90). Do ponto de vista matemático, você tem a mesma probabilidade de obter cara ou coroa.

Vamos calcular o Valor Esperado (EV) usando a fórmula conhecida e descobrir que nosso EV é negativo:

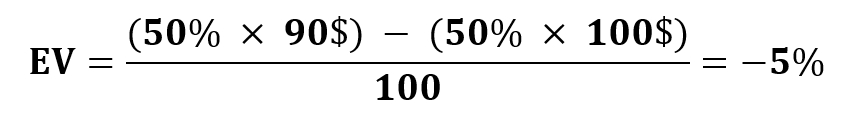
Isso significa que, a longo prazo, você terá uma média de prejuízo de -$5 para cada $100 apostados.

Portanto, toda vez que você obtém cara, recebe: 50 x $90 = $4500. Nos outros 50% dos casos, ocorre coroa, resultando na perda da aposta, totalizando 50 x $100 = $5000. Como resultado, o evento de jogar a moeda 100 vezes resulta em uma perda de $500. A longo prazo, você não conseguirá obter lucro. Este é um exemplo de aposta com Valor Esperado Negativo (-EV).

Exemplo de uma Aposta com Valor Esperado Positivo (+EV)

Agora, vamos assumir que encontramos uma moeda especial, na qual a probabilidade de obter cara é de 60% e a probabilidade de obter coroa é de 40%.

Vamos calcular o Valor Esperado (EV) usando a fórmula conhecida e descobrir que com essas probabilidades (60% e 40%), nosso EV é positivo:

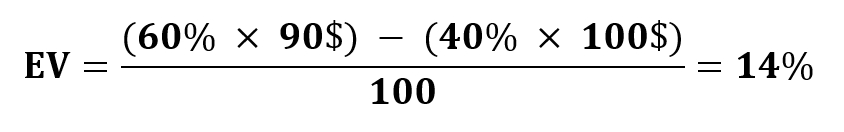
Isso significa que, a longo prazo, você terá uma média de lucro de +$14 para cada $100 apostados.

Em 100 lançamentos de moeda, obteremos cara 60 vezes, e receberemos 60 x $90 = $5400. Coroa ocorrerá 40 vezes, resultando em uma perda de 40 x $100 = $4000. No total, ficaremos com um lucro de $5400 – $4000 = $1400. Este é um exemplo de aposta com Valor Esperado Positivo (+EV).

É crucial não se desviar do plano e apostar em um resultado diferente. Ao lidar com apostas com Valor Esperado Positivo, é importante manter o rumo até o final!

Por que ocorrem as Value Bets (Apostas de Valor)?

Existem várias razões principais para o surgimento de Value Bets:

1. Análise incorreta de eventos esportivos futuros. Os analistas esportivos que trabalham para as casas de apostas também podem cometer erros ao prever o resultado de uma partida, especialmente quando se trata de ligas e equipes menos conhecidas.
2. Erros. As casas de apostas podem cometer erros ao definir as probabilidades, por exemplo, ao inserir acidentalmente 11 em vez de 1,1. No entanto, não recomendamos contar com probabilidades inflacionadas, pois há 99% de chance de a casa de apostas perceber e anular sua aposta.
3. Fatores aleatórios. No esporte, muitas vezes acontece de a equipe menos favorita vencer contra todas as previsões. Por exemplo, isso aconteceu quando a seleção nacional de futebol da Ucrânia venceu a seleção nacional da França.
4. As casas de apostas não reagem a mudanças no evento esportivo. Muitas vezes, elas não têm tempo para acompanhar as mudanças nas probabilidades. Isso leva a uma situação em que um jogador profissional aproveita as probabilidades favoráveis em uma casa de apostas que ainda não teve a chance de ajustar suas probabilidades.
5. Redução intencional das probabilidades. As casas de apostas podem reduzir intencionalmente as probabilidades definidas para certos resultados de um evento.

Como converter as odds de uma casa de apostas (EUA) em probabilidade %.

A seguir, descreveremos como converter as odds de uma casa de apostas (EUA) em probabilidade %.

Teams	ODDS
Team #1	+130
Team #2	-150

Para as odds dos EUA, se a linha da casa de apostas for positiva:

100 / (Bookmaker’s Line + 100) x 100%

Por exemplo, se a linha da casa de apostas for +130, divida 100 por (130 + 100):

100 / (130 + 100) x 100% = 43.48%

Para as odds dos EUA, se a linha da casa de apostas for negativa:

Bookmaker’s line / (Bookmaker’s line + 100) x 100%

Por exemplo, se a linha da casa de apostas for -150, divida 150 por (150 + 100) x 100%:

150 / (150 + 100) x 100% = 60%

Não calcule manualmente. Use um dos scanners!

O que é Vig no Valor Esperado (probabilidades no formato dos EUA)?

No contexto do Valor Esperado (EV) em apostas esportivas, “vig” refere-se à comissão da casa de apostas. Ao calcular o valor esperado de uma aposta, o vig é subtraído dos ganhos potenciais para levar em conta o lucro da casa de apostas. Ele representa a quantia que o apostador precisa superar para ficar no zero a zero ou obter lucro a longo prazo.

Como exemplo, vamos considerar uma competição entre a Equipe #1 e a Equipe #2. Nesse evento, há apenas um resultado possível – a vitória de uma das equipes. A casa de apostas oferece as seguintes probabilidades:

Teams	ODDS (US format)
Team #1	+130
Team #2	-150

Convertendo as odds da casa de apostas de +130 em probabilidade percentual:

100 / (130 + 100) x 100% = 43.48%

Convertendo as odds da casa de apostas de -150 em probabilidade percentual.

150 / (150 + 100) x 100% = 60%

Agora, vamos somar as odds e calcular o valor acumulado.

43.48% + 60% = 103.48%

Neste exemplo, o vig é calculado como 103,48% – 100% = 3,48%. Isso representa a margem da casa de apostas, que impede a lucratividade a longo prazo para os apostadores.

A existência do vig complica a busca pelo valor esperado porque você não está recebendo o que poderia ser considerado as verdadeiras probabilidades. Portanto, você precisa não apenas encontrar discrepâncias nas odds, mas também garantir que a discrepância seja maior que o valor do vig (em nosso caso, 3,48%). Somente então você estará em uma situação positiva. Se o seu valor for menor, a aposta não será mais uma aposta de +EV.

Como o Vig ajuda a calcular o lucro

Digamos que você esteja considerando uma aposta esportiva em uma partida de futebol, e a casa de apostas oferece as seguintes odds:

Team A: 2.00 (Even odds)

Team B: 1.90

Primeiro, calcule as probabilidades implícitas de cada resultado dividindo 1 pelas odds:

Probabilidade implícita de vitória da Equipe A: 1 / 2.00 = 0,50 (50%)

Probabilidade implícita de vitória da Equipe B: 1 / 1.90 = 0,5263 (52,63%)

Calcule o Vig:

Vig = (50% + 52.63%) - 100% = 2.63%.

Agora, subtraia o vig das probabilidades implícitas:

Probabilidade ajustada de vitória da Equipe A: 0,50 – 0,0263 = 0,47 (47%)

Probabilidade ajustada de vitória da Equipe B: 0,5263 – 0,0263 = 0,50 (50%)

Por fim, calcule o valor esperado multiplicando as probabilidades ajustadas pelos ganhos potenciais:

Valor Esperado (EV) de apostar na Equipe A: (0.47 * 2.00) - 1 = -0.06 (-6%)

Valor Esperado (EV) de apostar na Equipe B: (0.5 * 1.90) - 1 = -0.05 (-5%)

Neste exemplo, os valores esperados negativos indicam que nenhuma aposta oferece um retorno esperado positivo. O vig, neste caso, reduz a potencial lucratividade das apostas e é considerado no cálculo do valor esperado.

Como Encontrar e Calcular o Valor Esperado Positivo (EV) — Exemplo #1 (Para odds dos EUA)

A fórmula para calcular o Valor Esperado é relativamente simples:

A fórmula do Valor Esperado (EV): Valor Esperado = ([Porcentagem implícita de vitória] * [Lucro em caso de vitória]) - ([Porcentagem implícita de derrota] * [Valor apostado]).

Vamos considerar uma partida de futebol entre Liverpool e Barcelona com as seguintes odds:

	Barcelona	Liverpool
American/Moneyline format	-120	+100
Decimal format	1.83	2

Vamos calcular as probabilidades implícitas pela Bet360 para cada uma de suas linhas (Probabilidade).

Temos um próximo jogo na Bet360 entre o Barcelona e o Liverpool. Veja como a Bet360 vê a aposta na linha de vitória para cada equipe em termos de probabilidade implícita.

A Bet360 acredita que o “Barcelona” tem uma chance de vitória de:

120 / (120 + 100) x 100% = 54,5% (Probability = 0.545)
Por favor, escreva em inglês (-120): Bookmaker’s line / (Bookmaker’s line + 100) x 100%

A Bet360 acredita que o “Liverpool” tem uma chance de vitória de:

100 / (100 + 100) x 100% = 50% (Probability = 0.5)
Por favor, escreva em inglês (+100): 100 / (Bookmaker’s line + 100) x 100%

	Barcelona	Liverpool
American/Moneyline format	-120	+100
Decimal format	1.83	2
Probability	54.5%(0.545)	50%(0.5)

Vamos calcular o Vig com base nas odds calculadas.

Vemos que o total é de 104,5%. Isso se deve à margem que a casa de apostas cobra (essencialmente sua comissão — Vig) nesse mercado.

Vig=104.5% - 100% = 4.5%

Vamos calcular o Valor Esperado (EV).

Valor Esperado = (Probabilidade de Vitória x Valor a ser ganho por aposta) - (Probabilidade de Derrota x Valor a ser perdido por aposta)

O Valor Esperado para uma aposta de $100 no Barcelona é calculado da seguinte forma:

EV = (0,545 x $83) – (0,5 x $100) = -4,76$

Um valor esperado negativo aqui implica que o jogador perderá uma média de -$4.76 para cada $100 apostados no Barcelona.

Vamos assumir que estamos superestimando a probabilidade de vitória do Barcelona.

Vamos assumir que analisamos minuciosamente ambas as equipes e podemos especular que o “Barcelona” tem uma maior chance de vencer do que a Bet360 alega. Temos confiança de que as chances do «Barcelona» são de 60%, enquanto as chances do «Liverpool» são de 44,5% (para manter o total de 104,5%).

O Valor Esperado para uma aposta de $100 no Barcelona (60%) é calculado da seguinte forma:

EV = (0,6 x $83) – (0,445 x $100) = +$5,3

Um valor esperado positivo aqui significa que o jogador ganhará uma média de +$5.3 para cada $100 apostados no Barcelona.

Attention

A dificuldade está em determinar a probabilidade real de um evento. Jogadores regulares determinam a probabilidade real com base nas odds oferecidas por casas de apostas confiáveis. Em seguida, eles calculam se uma aposta é valiosa ou não usando uma fórmula específica. Para mais informações sobre essa metodologia para encontrar apostas valiosas, consulte a seção: “Como os Scanners de Apostas de Valor Funcionam”.

As odds reais para probabilidades de 60% e 44,5%.

Se definirmos as odds de apostas com base nessas probabilidades (60% e 44,5%), ficaria assim:

Barcelona: 150 / (150 + 100) x 100% = 60%

Liverpool: 100 / (125 + 100) x 100% = 44.5%

Por favor, escreva em inglês.

	Barcelona	Liverpool
American/Moneyline format	-150	+125
Decimal format	1.67	2.25
Probability	60% (0.6)	44.5% (0.445)

Com base nos cálculos acima, entendemos que as odds reais deveriam ter sido as seguintes: -150 para o “Barcelona” e +125 para o “Liverpool”. No entanto, a casa de apostas Bet360 definiu suas odds incorretamente: -120 para o “Barcelona” e +100 para o “Liverpool”, o que significa que consideramos ter encontrado uma aposta valiosa.

Experimente o Melhor Software para Busca Automatizada de Apostas +EV:

Calculando o Valor Esperado Positivo — Exemplo #2 (Para odds Europeias)

Para começar, você precisa converter as “Odds” em “Probabilidade.” Para fazer essa conversão, podemos usar a fórmula:

V = (1/K) x 100,
onde V é a probabilidade em porcentagem e K são as odds da casa de apostas.

Mas precisamos calcular não apenas as probabilidades atribuídas pela casa de apostas, mas também as nossas próprias. Nesse caso, o valor da aposta pode ser calculado usando a seguinte fórmula:

Val = VG / VB, 
onde VG representa a probabilidade do jogador e VB representa a probabilidade da casa de apostas.

Se Val for maior que 1, então você encontrou uma aposta de valor na qual você deve fazer uma aposta.

Vamos considerar uma partida de futebol entre Manchester City e Liverpool, onde o resultado é a vitória do Manchester City sobre o Liverpool. A casa de apostas definiu as odds para esse resultado em 2.25, enquanto avaliamos o evento com odds de 1.8. Vamos tentar calcular a probabilidade do resultado e determinar o valor de nossa aposta:

VB = (1/2,25) x 100 = 44,44%
VG = (1/1,8) x 100 = 55,55%
Val = 55,55% / 44,44% = 1,25

A partir do cálculo, é evidente que Val está acima de 1. Portanto, encontramos uma aposta de valor. Podemos fazer nossa aposta com confiança.

Calculando Valor Esperado Positivo — Exemplo #3

Calcular apostas de valor envolve avaliar a probabilidade de um resultado e compará-la com as odds oferecidas por uma casa de apostas. Aqui está um exemplo de como calcular apostas de valor:

1. Determinar a probabilidade: Comece estimando a probabilidade de um evento ocorrer. Isso pode ser baseado em análises estatísticas, desempenho da equipe ou quaisquer fatores relevantes. Digamos que você acredite que há 70% de chance de o Time A vencer uma partida de futebol.
2. Converter a probabilidade em odds: Converta a probabilidade estimada em odds decimais. Para calcular as odds, divida 1 pela probabilidade e multiplique por 100. Em nosso exemplo, as odds para o Time A seriam 1 / 0.70 * 100 = 1.43.
3. Comparar com as odds da casa de apostas: Verifique as odds oferecidas por uma casa de apostas para o mesmo evento. Suponha que a casa de apostas ofereça odds de 1.60 para o Time A vencer.
4. Calcular o valor: Calcule o valor subtraindo 1 das odds calculadas (passo 2) e dividindo pelo valor das odds da casa de apostas (passo 3). Em nosso exemplo, (1.43 – 1) / 1.60 = 0.27.
5. Avaliar o valor: Se o valor calculado no passo 4 for maior que 0, indica uma aposta de valor positivo. Um valor acima de 0 sugere que as odds oferecidas pela casa de apostas são maiores do que a probabilidade estimada, indicando potencial valor na aposta.

Neste exemplo, o valor calculado é 0.27, indicando uma aposta de valor positivo. Isso significa que as odds oferecidas pela casa de apostas são maiores do que a probabilidade estimada do Time A vencer, sugerindo que pode ser uma aposta favorável a fazer.

Como Funcionam os Scanners de Apostas de Valor

Apostas de valor são apostas realizadas em odds que, a longo prazo, proporcionam um resultado positivo. Isso acontece porque as odds para apostas de valor são mais altas do que as odds oferecidas pela “linha global” (a “linha global” reflete a probabilidade de vencer a aposta que está próxima da realidade).

Para buscar esses resultados, os scanners de apostas de valor utilizam a seguinte fórmula, comparando as odds da casa de apostas com as odds fornecidas por casas de apostas de referência, sem levar em conta a margem embutida nestas últimas:

EV = (1 / Odds da casa de apostas para cálculo x Pagamento) - (1 / Odds da casa de apostas para exibição x 100)

Por que sem margem? A questão é que as odds (de acordo com a casa de apostas para exibição) podem ser consideradas inflacionadas apenas se forem mais altas do que as odds que determinam a probabilidade real (ou seja, sem a margem incluída).

Exemplo de busca por odds inflacionadas:

	Odds	Payout
Bookmaker for calculation #1	1.65	92.5
Bookmaker for calculation #2	1.75	94.5
Bookmaker for calculation #3	1.73	95.0
Bookmaker for display	1.89	100

1. O bookmaker para exibição é o bookmaker usado para buscar apostas de valor (odds inflacionadas).
2. Os bookmakers para cálculo (bookmakers de referência) são os bookmakers em relação aos quais a busca por uma aposta com vantagem sobre o bookmaker escolhido para exibição será realizada.
3. Pagamento é o valor de retorno ao apostar em resultados opostos com um total de soma de 100.

Em outras palavras, quanto maior a margem do escritório da casa de apostas, menor será o pagamento. No bookmaker para exibição, o pagamento para nossa fórmula será igual a 100.

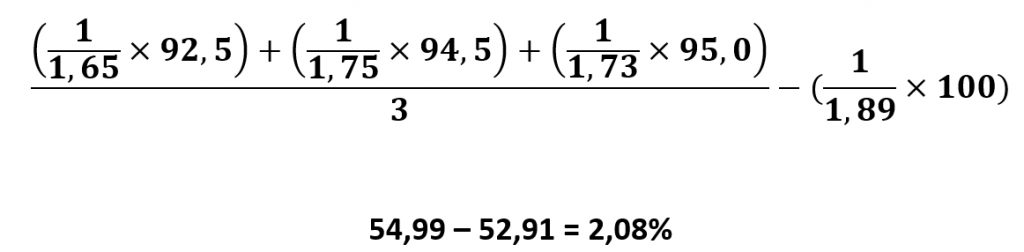
Com base nos cálculos acima, podemos ver que as odds de 1.89 estão inflacionadas em 2.08%. Em outras palavras, neste caso, estamos enganando a casa de apostas em 2.08% porque a linha deles está errônea (determinamos isso comparando as odds para um resultado específico entre nossa casa de apostas e várias casas de apostas de referência).

Agora vamos calcular o lucro potencial. Ao fazer 100 apostas de $100 cada com uma taxa de juros inflacionada de 2.08%, podemos potencialmente ganhar $208. Portanto, fazendo 3-4 apostas por dia com uma taxa de juros de 2.08%, começando com um bankroll de $300-400, após 100 apostas, alcançaríamos um lucro líquido de $208.

Este é o princípio pelo qual funciona o software de apostas com EV positivo (ele compara as odds em uma casa de apostas selecionada com as odds de casas de apostas de referência). Em seguida, ele calcula usando uma fórmula simples e fornece o resultado final.

Critérios importantes para a escolha do software

Lista dos critérios mais importantes:

➕ Plano gratuito	Até 1%
➕ Modo ao vivo	Sim ou Não
➕ Velocidade de digitalização	Apenas rápido
➕ Número de corretores	80 ou mais
➕ Número de mercados	100 ou mais
➕ Apostas de valor	Sim ou Não

Melhor software de apostas com EV positivo.

No final

Ao fazer consistentemente apostas com valor esperado positivo, os apostadores visam maximizar seus lucros ao longo do tempo. No entanto, é importante observar que mesmo com apostas de EV positivo, não há garantias de ganhar no curto prazo devido à variância inerente às apostas e aos resultados esportivos. O sucesso nas apostas com EV requer disciplina, gerenciamento de bankroll e uma perspectiva de longo prazo.

Literatura utilizada, referências

• How do you find value bets when betting on sports? // Quora.com
• What is value bet, and how do I win with value bet? // Quora.com
• Expected Value // en.wikipedia.org
• Value Bets Guide // Betburger.com