What is Positive Expected Value (EV) in Sports Betting?

Expected Value (EV) Betting is a sports betting strategy based on looking for a gap between the true odds of something happening and the odds published by the bookmaker. Expected Value (Value Bets) represents the average amount of money that a bettor can expect to win or lose on a specific bet over the long run. It takes into account the probability of winning or losing and the potential payout. By calculating the expected value, a bettor can determine whether a particular bet is potentially profitable or not.

A negative -EV in sports betting is a situation where the expected return from the bet is negative. It means that the probability of winning in the game is lower than expected.

A positive +EV in sports betting is a bet that will be profitable in the long run. It means that such a bet will win more than it loses in the long-term perspective (for example, by consistently betting at -110 odds, you will ultimately make a profit after 100 bets). The probability of winning this bet is usually higher than what the bookmaker assumes.

Using this strategy, the player will lose some bets. However, in the long run, they will still come out ahead. That’s why it is crucial to stick to the strategy until the end.

A Simpler Explanation with an Example

Brief explanation of American odds:

1. In the American odds system, the number on the line increases as the probability of winning decreases, and the number on the line decreases as the probability of winning increases.
2. This means that an underdog at +100 has a higher probability of winning than an underdog at +240 (according to the bookmaker). Conversely, a favorite at -190 has a greater chance of winning than a favorite at -120.

Example of a Bet with a Negative Expected Value (-EV)

Let’s consider the event of “flipping a coin.” You flipped a coin 100 times, and each time you placed a bet of $100 on tails with odds of -110 (a $100 bet yields a win of $90). From a mathematical standpoint, you have an equal chance of getting heads or tails.

Let’s calculate EV using the known formula and find out that our EV is negative:

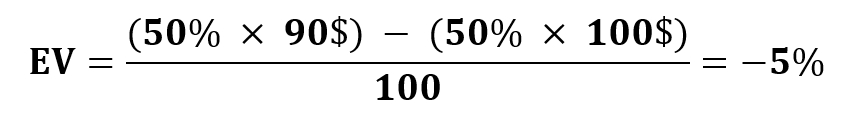
This means that in the long run, you will be averaging a loss of -$5 for every $100 wagered.

Therefore, every time you get heads, you receive: 50 x $90 = $4500. In the remaining 50% of cases, tails will occur, resulting in a loss of the bet, totaling 50 x $100 = $5000. As a result, the event of flipping the coin 100 times results in a loss of $500. In the long run, you won’t be able to make a profit. This is an example of a bet with a negative expected value (-EV).

Example of a Bet with a Positive Expected Value (+EV)

Now, let’s assume that we have found a special coin where the probability of getting heads is 60% and the probability of getting tails is 40%.

Let’s calculate EV using the known formula and find out that with these probabilities (60% and 40%), our EV is positive:

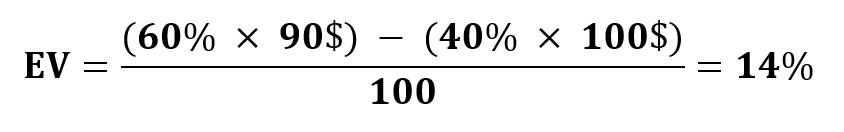
This means that in the long run, you will be averaging a profit of +$14 for every $100 wagered.

In 100 coin flips, heads will occur 60 times, and we will receive 60 x $90 = $5400. Tails will occur 40 times, resulting in a loss of 40 x $100 = $4000. In total, we will be left with a profit of $5400 – $4000 = $1400. This is an example of a bet with a positive expected value (+EV).

It is crucial not to deviate from the plan and bet on a different outcome. When dealing with bets with a positive expected value, it is important to stay the course until the end!

Why Do Value Bets Occur?

There are several main reasons for the emergence of Value Bets:

1. Incorrect analysis of upcoming sporting events. Sports analysts working for bookmakers can also make mistakes in predicting the outcome of a match, especially when it comes to lesser-known leagues and teams.
2. Errors. Bookmakers may make mistakes in writing odds, for example, by mistakenly entering 11 instead of 1.1. However, we do not recommend relying on inflated odds because there is a 99% chance that the bookmaker will notice it and void your bet.
3. Random factors. In sports, it often happens that the underdog team wins against all predictions. For example, this was the case when the Ukrainian national football team defeated the French national team.
4. Bookmakers fail to react to changes in the sporting event. They often do not have time to track changes in odds. This leads to a situation where a professional player takes advantage of favorable odds at a bookmaker who hasn’t had a chance to adjust their odds yet.
5. Intentional lowering of odds. Bookmakers may intentionally lower the odds set for certain outcomes of an event.

How to convert bookmaker odds (USA) into probability %.

Below we will describe how to convert bookmaker odds (USA) into probability%.

	ODDS
Team #1	+130
Team #2	-150

For US odds, if the bookmaker’s line is positive:

100 / (Bookmaker’s Line + 100) x 100%

For example, if the bookmaker’s line is +130, then divide 100 by (130 + 100):

100 / (130 + 100) x 100% = 43.48%

For US odds, if the bookmaker’s line is negative: 

Bookmaker’s line / (Bookmaker’s line + 100) x 100%

For example, if the bookmaker’s line is -150, then divide 150 by (150 + 100) x 100%:

150 / (150 + 100) x 100% = 60%

Don’t calculate manually. Use one of the scanners!

What is Vig in Expected Value (US format odds)?

In the context of Expected Value (EV) in sports betting, “vig” refers to the bookmaker’s commission. When calculating the expected value of a bet, the vig is subtracted from the potential winnings to account for the bookmaker’s profit. It represents the amount that the bettor needs to overcome in order to break even or make a profit in the long run.

As an example, let’s consider a competition between Team #1 and Team #2. In this event, there is only one outcome – the victory of one of the teams. The bookmaker offers the following odds:

	ODDS (US format)
Team #1	+130
Team #2	-150

Converting the bookmaker odds of +130 into a percentage probability:

100 / (130 + 100) x 100% = 43.48%

Converting the bookmaker odds of -150 into a percentage probability.

150 / (150 + 100) x 100% = 60%

Now let’s add the odds together and calculate the cumulative value.

43.48% + 60% = 103.48%

In this example, the vig is calculated as 103.48% – 100% = 3.48%. This represents the bookmaker’s margin, which prevents long-term profitability for bettors.

The existence of Vig complicates the search for expected value because you are not receiving what could be considered the true odds. Therefore, you need to not only find discrepancies in the odds but also ensure that the discrepancy is greater than the Vig value (in our case, 3.48%). Only then will you be in a positive situation. If your value is lower, it will no longer be a +EV bet.

How Vig Helps to Calculate Profit

Let’s say you’re considering a sports bet on a football game, and the bookmaker offers the following odds:

Team A: 2.00 (Even odds)

Team B: 1.90

First, calculate the implied probabilities of each outcome by dividing 1 by the odds:

Implied probability of Team A winning: 1 / 2.00 = 0.50 (50%)

Implied probability of Team B winning: 1 / 1.90 = 0.5263 (52.63%)

Calculate the Vig:

Vig = (50% + 52.63%) - 100% = 2.63%.

Now, subtract the vig from the implied probabilities:

Adjusted probability of Team A winning: 0.50 – 0.0263 = 0.47 (47%)

Adjusted probability of Team B winning: 0.5263 – 0.0263 = 0.5 (50%)

Finally, calculate the expected value by multiplying the adjusted probabilities by the potential winnings:

EV of betting on Team A: (0.47 * 2.00) - 1 = -0.06 (-6%)

EV of betting on Team B: (0.5 * 1.90) - 1 = -0.05 (-5%)

In this example, the negative expected values indicate that neither bet offers a positive expected return. The vig, in this case, reduces the potential profitability of the bets and is factored into the expected value calculation.

How to Find & Calculate Positive EV — Example #1 (For US odds)

The formula for calculating EV is relatively simple:

The formula ov EV: Expected Value = ([Winning implied probability %] * [Profit if bet won]) – ([Losing implied probability %] * [Stake]).

Let’s consider a football match between Liverpool and Barcelona with the following odds:

	Barcelona	Liverpool
American/Moneyline format	-120	+100
Decimal format	1.83	2

Let’s calculate the odds implied by Bet360 for each of its lines (Probability).

We have an upcoming Bet360 game between the Barcelona and the Liverpool. See how Bet360 sees the moneyline bet in terms of implied probability. 

Bet360 believes that «Barcelona» has a chance of winning of:

120 / (120 + 100) x 100% = 54,5% (Probability = 0.545)
formula for negative odds (-120): Bookmaker’s line / (Bookmaker’s line + 100) x 100%

Bet360 believes that «Liverpool» has a chance of winning of:

100 / (100 + 100) x 100% = 50% (Probability = 0.5)
formula for posetive odds (+100): 100 / (Bookmaker’s line + 100) x 100%

	Barcelona	Liverpool
American/Moneyline format	-120	+100
Decimal format	1.83	2
Probability	54.5%(0.545)	50%(0.5)

Let’s calculate the Vig based on the calculated odds.

We see that the total is 104.5%. This is due to the margin that the bookmaker charges (essentially their commission — Vig) on that market.

Vig=104.5% - 100% = 4.5%

Let’s calculate the EV.

Expected Value = (Probability of Winning x Amount to be won per bet) – (Probability of Losing x Amount to be lost per bet)

The Expected Value for a $100 bet on the Barcelona is calculated as follows:

EV = (0,545 x $83) – (0,5 x $100) = -4,76$

A negative expected value here implies that the player will lose an average of -$4.76 for every $100 wagered on Barcelona.

Let’s assume that we are overestimating the probability of Barcelona winning.

Let’s assume that we have thoroughly analyzed both teams and can speculate that “Barcelona” has a higher chance of winning than what Bet360 claims. We are confident that the chances of «Barcelona» are 60%, while the chances of «Liverpool» are 44.5% (to maintain the total of 104.5%).

The Expected Value for a $100 bet on the Barcelona (60%) is calculated as follows:

EV = (0,6 x $83) – (0,445 x $100) = +$5,3

A positive expected value here means that the player will win an average of +$5.3 for every $100 wagered on Barcelona.

Attention

The difficulty lies in determining the actual probability of an event. Regular players determine the real probability based on the odds offered by reputable bookmakers. They then calculate whether a bet is valuable or not using a specific formula. For more information on this methodology for finding valuable bets, please refer to the section: “How Value Bet Scanners Work“.

The actual odds for probabilities of 60% and 44.5%.

If we were to set the betting odds based on these probabilities (60% and 44.5%), it would look like this:

Barcelona: 150 / (150 + 100) x 100% = 60%

Liverpool: 100 / (125 + 100) x 100% = 44.5%

Let’s draw a new table:

	Barcelona	Liverpool
American/Moneyline format	-150	+125
Decimal format	1.67	2.25
Probability	60% (0.6)	44.5% (0.445)

Based on the calculations above, we understand that the actual odds should have been as follows: -150 for «Barcelona» and +125 for «Liverpool». However, the bookmaker Bet360 has set their odds incorrectly: -120 for «Barcelona» and +100 for «Liverpool», which means that we consider we have found a valuable bet.

Try the Best Software for Automated Searching for +EV Bets:

Calculating Positive Expected Value — Example #2 (For European odds)

To begin, you need to convert “Odds” into “Probability.” To make this conversion, we can use the formula:

V = (1/K) x 100,
where V is the probability in percentage and K is the bookmaker's odds.

But we need to calculate not only the bookmaker’s assigned probabilities but also our own. In that case, the value of the bet can be calculated using the following formula:

Val = VG / VB, 
where VG represents the player's probability and VB represents the bookmaker's probability.

If Val is greater than 1, then you have found a value bet that you should place a wager on.

Let’s consider a football match between Manchester City and Liverpool, where the outcome is Manchester City’s victory over Liverpool. The bookmaker has set the odds for this outcome at 2.25, while we have evaluated the event with odds of 1.8. Let’s try to calculate the probability of the outcome and determine the value of our bet:

VB = (1/2,25) x 100 = 44,44%
VG = (1/1,8) x 100 = 55,55%
Val = 55,55% / 44,44% = 1,25

From the calculation, it is evident that Val is above 1. Therefore, we have found a value bet. We can confidently place our wager.

Calculating Positive Expected Value — Example #3

Calculating value bets involves assessing the probability of an outcome and comparing it to the odds offered by a bookmaker. Here’s an example of how to calculate value bets:

1. Determine the probability: Start by estimating the probability of an event occurring. This can be based on statistical analysis, team performance, or any relevant factors. Let’s say you believe there is a 70% chance of Team A winning a football match.
2. Convert probability to odds: Convert the estimated probability into decimal odds. To calculate the odds, divide 1 by the probability and multiply by 100. In our example, the odds for Team A would be 1 / 0.70 * 100 = 1.43.
3. Compare with bookmaker odds: Check the odds offered by a bookmaker for the same event. Suppose the bookmaker offers odds of 1.60 for Team A to win.
4. Calculate the value: Calculate the value by subtracting 1 from the odds you calculated (step 2) and dividing it by the bookmaker’s odds (step 3). In our example, (1.43 – 1) / 1.60 = 0.27.
5. Assess the value: If the value calculated in step 4 is greater than 0, it indicates a positive value bet. A value above 0 suggests that the odds offered by the bookmaker are higher than the estimated probability, indicating potential value in the bet.

In this example, the value calculated is 0.27, indicating a positive value bet. This means the odds offered by the bookmaker are higher than the estimated probability of Team A winning, suggesting it may be a favorable bet to make.

How Value Bet Scanners Work

Value bets are bets placed on odds that, in the long run, yield a positive result. This is due to the fact that the odds for value bets are higher than the odds offered by the “global line” (the “global line” reflects the probability of winning the bet that is close to reality).

To search for such outcomes, value bet scanners utilize the following formula, comparing the bookmaker’s odds against the odds provided by benchmark bookmakers, without taking into account the built-in margin in the latter:

EV = (1 / Bookmaker's odds for calculation x Payout) - (1 / Bookmaker's odds for display x 100)

Why without margin? The thing is, the odds (according to the bookmaker for display) can be considered inflated only if they are higher than the odds determining the actual probability (i.e., without the included margin).

Example of searching for inflated odds:

	Odds	Payout
Bookmaker for calculation #1	1.65	92.5
Bookmaker for calculation #2	1.75	94.5
Bookmaker for calculation #3	1.73	95.0
Bookmaker for display	1.89	100

1. Bookmaker for display is the bookmaker used for searching Valuebets (inflated odds).
2. Bookmakers for calculation (benchmark bookmakers) are the bookmakers against which the search for a bet with an advantage on the chosen bookmaker for display will be conducted.
3. Payout is the amount of return when betting on opposite outcomes with a total sum of 100.

In other words, the higher the margin of the bookmaker’s office, the lower the payout. In the bookmaker for display, the payout for our formula will be equal to 100.

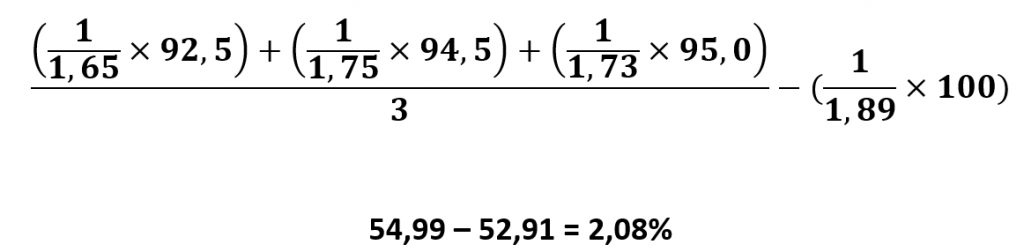
Based on the calculations above, we can see that the odds of 1.89 are inflated by 2.08%. In other words, in this case, we are outsmarting the bookmaker by 2.08% because their line is erroneous (we determined this by comparing the odds for a specific outcome between our bookmaker and several benchmark bookmakers).

Now let’s calculate the potential profit. By placing 100 bets of $100 each with an inflated interest rate of 2.08%, we can potentially earn $208. Therefore, by making 3-4 bets per day at 2.08% interest rate, starting with a bankroll of $300-400, after 100 bets, we would achieve a net profit of $208.

This is the principle on which positive ev betting software works (it compares the odds in a selected bookmaker with the odds from benchmark bookmakers). Then, it calculates using a simple formula and provides the final result.

Important criteria for choosing software

List of the most important criteria:

➕ Free plan	Up to 1%
➕ Live mode	Yes or No
➕ Scan speed	Only Fast
➕ Number of bookies	80 or more
➕ Number of markets	100 or more
➕ Valuebets	Yes or No

Best Positive EV Betting Software

In The End

By consistently making bets with positive expected value, bettors aim to maximize their profits over time. However, it is important to note that even with positive EV bets, there are no guarantees of winning in the short term due to the inherent variance in gambling and sports outcomes. Success in EV betting requires discipline, bankroll management, and a long-term perspective.

Used literature, references

• How do you find value bets when betting on sports? // Quora.com
• What is value bet, and how do I win with value bet? // Quora.com
• Expected Value // en.wikipedia.org
• Value Bets Guide // Betburger.com